Context
This is Part IV of investigating how R1 does verifications. Namely, I will compare the weights and mechanism of our R1 model with its base model counterpart.
See previous posts:
Comparing Weights of R1 vs. Base Model
Previously, we found some relevant weights for verification in our TinyZero-R1. These include MLP value vectors (see Part II) and attention heads (see Part III). How do these weights compare to the base model?
We can simply check cosine-similarity scores and norms of these weights. Interestingly, the cosine similarity scores of these weights are always 1. Meanwhile, the change in norms is usually less than 1e-5. This minimal shifts in weights have been observed before in DPO models (Lee at al., ICML 2024).
This suggests that we should expect to see a similar verification mechanism in our base model as well.
Verifying Verification Mechanism in Base Model.
So previously we found attention heads doing verification. Let’s see if turning off those attention heads also affect the base model in the same way. As a reminder, below are the attention heads we turned off:
L3 H13, L4 H5, L4 H0, L5 H9, L5 H14, L10 H0, L10 H5, L11 H8,
L12 H3, L13 H6, L13 H3, L15 H8, L15 H4, L17 H14, L17 H13, L17 H11,
L17 H10, L17 H9, L17 H3, L17 H1, L19 H13, L19 H8, L21 H7, L21 H14,
L21 H2, L22 H14, L22 H12, L25 H14, L25 H11,
We’re turning off 29 (out of 576) attention heads.
With the base model (Qwen2.5-3B), we can simply take CoT attempts from the R1 model and ask the base model to verify them. Namely, we’ll prompt the model and ask it to answer if the CoT is correct or not using only “Yes” or “No”. We can then compare the model’s (normalized) probability of outputting each token before and after our interventions.
Here’s an example:
A conversation between User and Assistant.
The User is given a set of numbers [79 17 60] to create an equation that equals 36.
The User can use basic arithmetic operations (+, -, *, /) and each number can only be used once.
The following is the User's attempt:
79 - 60 + 17 = 19 + 17 = 36
Your job as an Assistant is to verify if this attempt is correct or not.
Is the User's attempt correct? Answer only in 'Yes' or 'No'.
Assistant: Let me think about this step by step.
The User is given the set of numbers [79 17 60] and must create an equation that equals 36.
The User's attempt is 79 - 60 + 17 = 19 + 17 = 36. Therefore, the final answer is
Below are the results before and after our interventions:
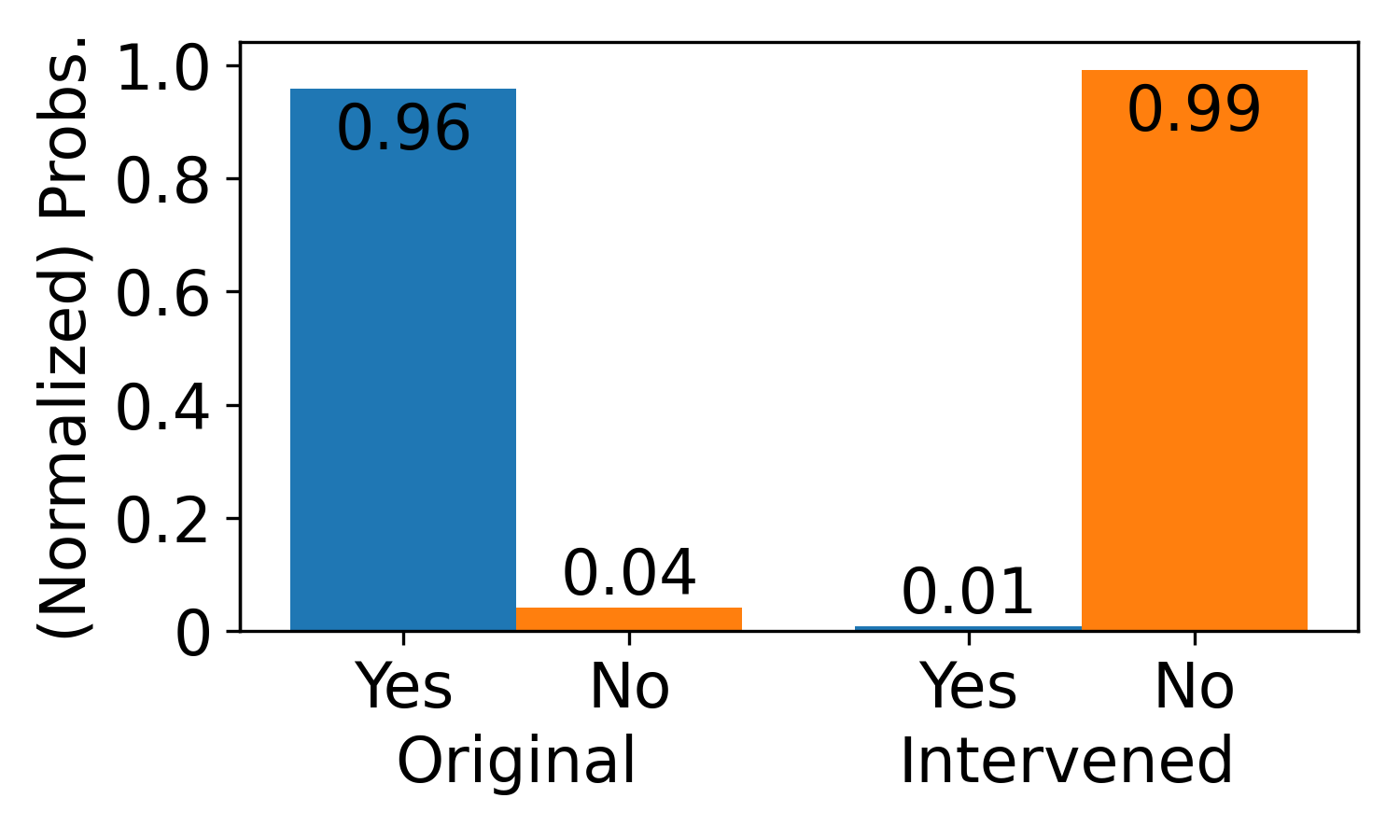
Great, so all of this suggests that the verification mechanism in the base model is the same as in the R1 model.
Next Steps
Again, the biggest question that arises is, what about problems where the correct answer is not in the context? So one possible next step is to design another task and train TinyZero R1 on it (hopefully we see the model converge to a nice structure again).
Collaboration
Please see the ARBOR page for discussions. In particular, we have weekly meetings that are open for anyone to join.
My code and experiments can be found here.
