Context
This is Part III of investigating how R1 does verifications. See Part I and Part II.
(Recap from Part I) Model:
As a reminder, we are working with a model trained on a specific reasoning task (a countdown task). Given 3 or 4 “operand” numbers (ex: 67, 90, 60, 12) and a target number (ex: 49), R1 needs to find an arithmetic combination that produces the target number. See Part I for details.
Luckily, this means we know the exact token to look for when the model has found a solution. Namely, the model always outputs in a structured format:
- 90 - 67 - 60 + 12 = -15 (not 49)
- 90 - 67 + 60 - 12 = 71 (not 49)
- 90 - 67 + 12 - 60 = -15 (not 49)
- 90 - 60 - 12 + 67 = 85 (not 49)
- 67 + 60 - 90 - 12 = 25 (not 49)
- 67 + 90 - 60 - 12 = 85 (not 49)
- 67 + 90 + 12 - 60 = 109 (not 49)
- 67 + 60 + 12 - 90 = 49 (this works)
So, the equation that equals 49 is 67 + 60 + 12 - 90. </think>
<answer> (67 + 60 + 12) - 90 </answer><|endoftext|>
Thus, we have a specific timestep (right when a “(“ is predicted, and when “this” will be predicted next) where we can do a deep dive.
In Part II, we looked at how MLP value vectors promote the likelihood of tokens such as “success” or “yes”, or “incomplete” or “failed”.
In this post we will look at the role of attention in verification.
Attention Heads
Since our model outputs are nicely structured, we simply have to inspect the attention patterns right after the model has outputted the correct numeric answer.
Consider the following example:
Using the numbers [11, 5, 68], create an equation that equals 62. ... (omitted) ...
Assistant: Let me solve this step by step.
<think> We have the numbers 11, 5, and 68. Let's try different combinations:
- 68 - 11 - 5 = 52 - 5 = 47 (not 62)
- 68 - 11 + 5 = 57 + 5 = 62 (this works)
Let’s look at the attention patterns right after 62 (the correct answer) is outputted. Here are interactive plots for attention patterns. Here is an example from layer 4 (though I encourage looking at the interactive plots!):
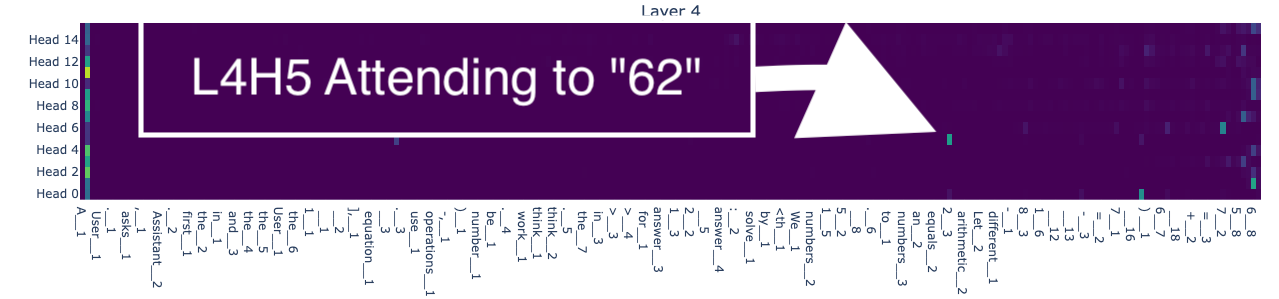
One thing you may notice is that some heads attend to the previous occurrences of the correct answer (62)!
Examples of this are L3H13, L4H0, L4H5, L5H9, and so on. A coincidence? Probably not!
So let’s try to turn off the “O-circuit” of these attention heads (i.e., these heads won’t be able to write into the residual stream). Here are the attention heads that I turned off:
L3 H13, L4 H5, L4 H0, L5 H9, L5 H14, L10 H0, L10 H5, L11 H8,
L12 H3, L13 H6, L13 H3, L15 H8, L15 H4, L17 H14, L17 H13, L17 H11,
L17 H10, L17 H9, L17 H3, L17 H1, L19 H13, L19 H8, L21 H7, L21 H14,
L21 H2, L22 H14, L22 H12, L25 H14, L25 H11,
(I just arbitrarily picked attention heads based on the visualization above. We will likely need a more systematic analysis later.)
And here is the output after turning off these attention heads:
Assistant: Let me solve this step by step.
<think> We have the numbers 11, 5, and 68. Let's try different combinations:
- 68 - 11 - 5 = 52 - 5 = 47 (not 62)
- 68 - 11 + 5 = 57 + 5 = **62 (not 62 - 11 + 5)**
- 68 - 11 + 5 = 57 + 5 = **62 (not 62 + 11 - 5)**
- 68 + 11 - 5 = 79 - 5 = 74 (not 62)
- 68 + 11 + 5 = 79 + 5 = 84 (not 62)
- 68 * 11 - 5 = 748 - 5 = 743 (not 62)
- 68 * 11 / 5 = 748 / 5 = 149.6 (not 62)
- 68 / 11 + 5 = 6.18 + 5 = 11.18 (not 62)
- 68 / 11 +
Note the text marked in asterisks – the model is now outputting the correct answer, but it is not recognizing it as such!
Relation to MLP Value Vectors
Previously, we identified MLP value vectors promoting tokens like “success” or “failed”. What is the relationship between the attention heads and MLP value vectors that we identified?
Here, we can simply compare the activation of the value vectors before and after the attention heads are turned off:
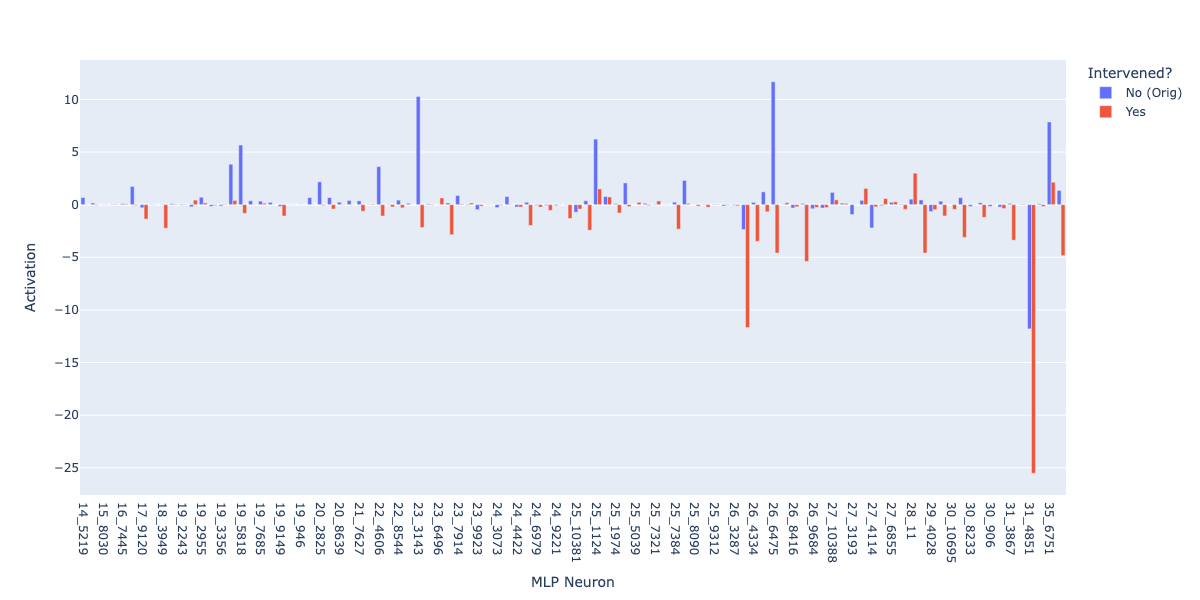
As you can see, the value vectors corresponding to “success” etc. are no longer activated when the attention heads are turned off. That is to say, I believe it is the attention heads that are responsible for activating the value vectors that promote tokens like “success”.
Next Steps
The biggest question that arises is, what about problems where the correct answer is not in the context? In hindsight, the mechanism we found is perhaps expected. So one possible next step is to design another task and train TinyZero R1 on it (hopefully we see the model converge to a nice structure again).
Another question is to compare the model before and after RL fine-tuning. IE, what were these attention heads doing before? Did the MLP value vectors change in any meaningful way from RL?
Alternatively, is the verification mechanism of the base model the same as the RL model? ie, Imagine giving the base model a prompt like the following: “We have numbers 11, 5, and 68. We need to find an equation that equals 62. Is 68 * 11 - 5 the solution? answer in yes or no” If we were to reverse engineer how the model answers this prompt, would we see the same mechanism as what we found in our model?
Lastly, we should probably set up a more systematic experiments to write up our findings in a potential paper.
Collaboration
Please see the ARBOR page for discussions. In particular, we have weekly meetings that are open for anyone to join.
My code and experiments can be found here.
